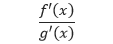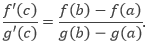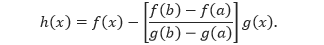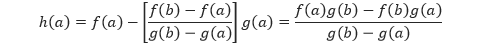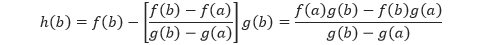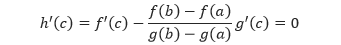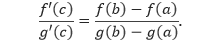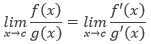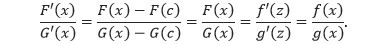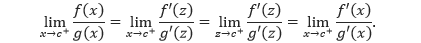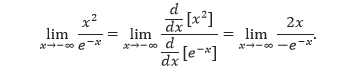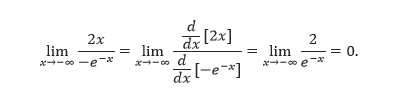Turunan implisit

Implisit adalah fungsi yang terdiri dari dua atau lebih variabel yakni variabel bebas dan variabel tak bebas, yang berada dalam satu ruas dan tidak bisa dipisahkan pada ruas yang berbeda.

Menurunkan fungsi implisit, tak jauh beda dengan menurunkan fungsi variabel tunggal, yakni dengan menggunakan notasi Leibniz (dy/dx). Berikut ini, hal yang harus dipahami dalam menurunkan fungsi implisit khususnya yang memiliki dua variabel (x dan y).

CONTOH 1

Tentukan $\frac{dy}{dx}$ dari $x{y}^2=x-8$.

Pembahasan

Pertama, kita turunkan kedua ruas terhadap $x$.$$\begin{array}{rl}\frac{d}{dx}(x{y}^2)& =\frac{d}{dx}(x-8)\end{array}$$

Karena $y$ merupakan suatu fungsi dalam $x$, maka $x{y}^2$ dapat dipandang sebagai perkalian dua buah fungsi, yang turunannya dapat dicari dengan menggunakan aturan perkalian. Misalkan $u=x$ dan $v=y^2$.$$\begin{array}{rl}u& =x⟹\frac{du}{dx}=1\\ v& =y^2⟹\frac{dv}{dx}=2y\cdot \frac{dy}{dx}\end{array}$$Sehingga$$\begin{array}{rl}\frac{d}{dx}(x{y}^2)& =u\cdot \frac{dv}{dx}+v\cdot \frac{du}{dx}\\ & =x\cdot 2y\cdot \frac{dy}{dx}+y^2\cdot 1\\ & =2xy\cdot \frac{dy}{dx}+y^2\end{array}$$

Dengan menentukan turunan dari suku lainnya, diperoleh

$$\begin{array}{rl}\frac{dx}{d}(x{y}^2)& \\ & =\frac{d}{dx}(x-8)\\ 2xy\cdot \frac{dy}{dx}+y^2& =1\\ 2xy\cdot \frac{dy}{dx}& =1-y^2\\ \frac{dy}{dx}& =\frac{1-y^2}{2xy}\end{array}$$

Diperoleh turunan pertama dari fungsi tersebut. Akan tetapi, apakah kita yakin dengan hasil yang diperoleh dengan turunan implisit? Agar lebih yakin, kita akan menentukan turunan sebuah fungsi dengan dua cara, kemudian membandingkan hasil yang diperoleh. Kita akan menggunakan fungsi implisit, yang pada awal pembahasan, turunannya dicari dengan mengubah fungsi tersebut ke dalam bentuk eksplisit. Fungsi tersebut adalah $4x^{2}y-xy=x^3+1$.

CONTOH 2

Tentukan $y^{\prime }=\frac{dy}{dx}$ dari $4x^{2}y-xy=x^3+1$ dengan turunan implisit.

Pembahasan

Pertama, kita turunkan kedua ruas terhadap x. Agar proses pengerjaan menjadi lebih sederhana, kita akan menggunakan notasi $y^{\prime }$ untuk menggantikan $\frac{dy}{dx}$.$$\begin{array}{rl}(8xy+4x^2{y}^{\prime })-(y+x{y}^{\prime })& =3x^2\\ 8xy+4x^2{y}^{\prime }-y-x{y}^{\prime }& =3x^2\\ 4x^2{y}^{\prime }-x{y}^{\prime }& =3x^2-8xy+y\\ (4x^2-x)y^{\prime }& =3x^2-8xy+y\\ y^{\prime }& =\frac{3x^2-8xy+y}{4x^2-x}\end{array}$$

Akhirnya, kita peroleh hasil dengan turunan implisit. Jika dilihat secara sekilas, hasil ini berbeda dari hasil yang diperoleh sebelumnya. Namun coba perhatikan, ternyata hasil ini masih memuat variabel y, sedangkan hasil yang kita peroleh sebelumnya hanya memuat variabel x. Kita ketahui bahwa$$\begin{array}{rl}y& =\frac{4x^2-x}{x^3+1}\end{array}$$

Substitusi nilai y pada hasil yang diperoleh dengan turunan implisit.$$\begin{array}{rl}{y}^{\prime }& =\frac{3x^2-8xy+y}{4x^2-x}\\ & =\frac{3x^2-8x\left(\frac{x^3+1}{4x^2-x}\right)+\left(\frac{x^3+1}{4x^2-x}\right)}{4x^2-x}\\ & =\frac{\frac{3x^2(4x^2-x)}{4x^2-x}-\frac{8x(x^3+1)}{4x^2-x}+\frac{x^3+1}{4x^2-x}}{4x^2-x}\\ & =\frac{\frac{(12x^4-3x^3)-(8x^4+8x)+(x^3+1)}{4x^2-x}}{4x^2-x}\\ & =\frac{\frac{4x^4-2x^3-8x+1}{4x^2-x}}{4x^2-x}\\ & =\frac{4x^4-2x^3-8x+1}{(4x^2-x{)}^2}\end{array}$$

sumber :

https://www.kimiamath.com/post/turunan-fungsi-implisit

Fungsi Diferensial dan Aturan Rantai

Pengertian

Kalkulus diferensial adalah salah satu cabang kalkulus dalam matematika yang mempelajari bagaimana nilai suatu fungsi berubah menurut perubahan input nilainya. Topik utama dalam pembelajaran kalkulus diferensial adalah turunan.

Aturan Rantai:

Jika f dan g merupakan fungsi yang dapat dideferensialkan ( turunkan ). F = f o g adalah fungsi dengan definisi F(x)=f ( g(x) ). Maka F dapat dideferensialkan menjadi sebagai berikut.

Apabila digunakan notasi Leibniz, dengan y = f(u) dan u = g(x). Aturan rantai dapat ditlis ulang menjadi

contoh soal :

Pada soal pertama ini, kita memiliki sebuah fungsi F(x) = (x^3+4x)^7. Dalam fungsi pangkat terdapat fungsi dengan bentuk x^3+4x. Kita definisikan u = x^3+4x . Sehingga dengan menerapkan aturan rantai, maka dapat kita peroleh.

sumber : https://chafias.com/kalkulus/aturan-rantai-turunan-contoh-dan-pembahasan/

Turunan L'hopital

Aturan L’Hôpital menyatakan bahwa dalam kondisi tertentu, limit dari pembagian f(x)/g(x) dapat ditentukan dengan menggunakan limit pembagian dari turunan-turunannya, yaitu

Untuk membuktikan teorema ini, digunakan Teorema Nilai Rata-rata yang Diperluas, seperti berikut.

TEOREMA NILAI RATA-RATA YANG DIPERLUASJika f dan g memiliki turunan pada interval terbuka (a, b) dan kontinu pada [a, b] sedemikian sehingga g’(x) ≠ 0 untuk setiap x di dalam (a, b), maka ada titik c di (a, b) sedemikian sehingga,

Bukti Kita dapat menganggap bahwa g(a) ≠ g(b), karena jika tidak, menurut Teorema Rolle, akan mengakibatkan g’(x) = 0 untuk suatu x di (a, b). Sekarang, didefinisikan h(x) sebagai berikut.

Maka

dan

dan dengan menggunakan Teorema Rolle, ada titik c di (a, b) sedemikian sehingga

yang menyebabkan bahwa,

Setelah membuktikan Teorema Nilai Rata-rata yang Diperluas, sekarang perhatikan Teorema L’Hôpital berikut.

ATURAN L’HÔPITALMisalkan f dan g adalah fungsi-fungsi yang memiliki turunan pada interval terbuka (a, b) yang memuat c, kecual pada c itu sendiri. Anggap g(x) ≠ 0 untuk setiap x di (a, b), kecuali pada c itu sendiri. Jika limit dari f(x)/g(x) untuk x mendekati c menghasilkan bentuk tidak tentu 0/0, maka

apabila limit di ruas kanan ada (atau tak hingga). Hasil ini juga dapat diterapkan jika limit f(x)/g(x) untuk x mendekati c menghasilkan bentuk-bentuk tak tentu ∞/∞, (–∞)/∞, ∞/(–∞), dan (–∞)/(–∞).

Seperti yang telah disinggung sebelumnya, Aturan L’Hôpital tersebut akan dibuktikan dengan menggunakan Teorema Nilai Rata-rata yang Diperluas. Karena banyak kasus dalam aturan ini, maka pada pembahasan ini hanya akan dibuktikan untuk satu kasus saja. Untuk kasus yang lain diserahkan kepada pembaca sebagai latihan.

Bukti Perhatikan satu kasus untuk,

Selanjutnya definisikan fungsi baru sebagai berikut.

Untuk setiap x, c < x < b, F dan G memiliki turunan pada (c, b] dan kontinu pada [c, b]. Sehingga, Teorema Nilai Rata-rata yang Diperluas dapat diterapkan untuk menyimpulkan bahwa ada bilangan z di (c, x) sedemikian sehingga

Akhirnya, dengan memisalkan x mendekati c dari kanan, x → c+, didapatkan z → c+karena c < z < x, dan

Catatan Kesalahan kadang-kadang dilakukan dengan menggunakan Aturan Turunan pada Pembagian f(x)/g(x) dalam menerapkan Aturan L’Hôpital ini. Pastikan bahwa aturan ini memuat f ’(x)/g’(x), bukan turunan dari f(x)/g(x). Selanjutnya perhatikan beberapa contoh berikut.

Contoh 1: Bentuk Tak Tentu 0/0

Tentukan nilai limit dari (e2x – 1)/x untuk x mendekati 0.

Pembahasan Karena dengan menggunakan substitusi langsung menghasilkan bentuk tak tentu 0/0,

sehingga dapat diterapkan Aturan L’Hôpital, seperti yang ditunjukkan di bawah ini.

Contoh 2: Penerapan Aturan L’Hôpital Lebih dari Satu Kali

Tentukan limit x2/e–x untuk x mendekati negatif tak hingga.

Pembahasan Karena dengan substitusi langsung akan menghasilkan bentuk tak tentu ∞/∞, maka gunakan Aturan L’Hôpital.

Limit ini masih menghasilkan bentuk tak tentu (–∞)/(–∞), sehingga Aturan L’Hôpital dapat diterapkan kembali.

sumber : https://yos3prens.wordpress.com/2013/09/12/aturan-lhopital/