KEBEBASAN LINEAR

penjelasan kebebasan linear

CIRI-CIRI BEBAS DAN BERGANTUNG LINEAR

●        Himpunan vector S bebas linier jika system persamaan linier hanya mempunyai penyelesaian trivial (nol).

●        Himpunan vector S bergantung linier jika system persamaan linier mempunyai persamaan non trivial.

●        Vektor S merupakan bebas linear apabila

1.  Matrik tersebut det(S) ≠ 0.

2.  Ketiga vector tersebut mempunyai invers (sehingga dapat dibalik)

contoh soal :

KOMBINASI LINEAR

contoh soal :

 a.       h = (4, 2, 6)
 b.       j = (1, 5, 6)

Jawab:

           ini juga dapat ditulis menjadi

          

CRAMER

Aturan Cramer untuk Sistem 3 × 3

Aturan Cramer dapat diperluas untuk sistem persamaan linear 3 × 3, dengan menggunakan pola yang sama dengan sistem 2 × 2. Diberikan sistem umum 3 × 3,

Solusi-solusi dari sistem tersebut adalah x = Dx/D, y = Dy/D, dan z = Dz/D, dimana Dx, Dy, dan Dz dibentuk dengan mengganti koefisien variable-variabel yang bersangkutan dengan konstanta, dan D adalah determinan dari matriks koefisien (D ≠ 0).

---

Penerapan Aturan Cramer untuk Sistem 3 × 3

Diberikan suatu sistem persamaan linear 3 × 3

Solusi dari sistem tersebut adalah (x, y, z), dimana

dengan syarat D ≠ 0.

CONTOH

RUANG VEKTOR DAN RUANG BAGIAN

Misalkan V adalah himpunan sembarang,V dikatakan ruang vektor bilamana aksioma-aksioma berikut dipenuhi :

1. jika u dan v verktor di V, maka u+v juga berada di V
2. u+v = v+u
3. u+(v+w) =(u+v)+w
4. ada sebuah vektor 0 di V sehingga 0+u = u+0
5. untuk setiap u di V terdapat -u di V sehingga u+(-u) = u+u=0
6. jika k dan skalar dan u di V, maka ku berada di V
7. k(u+v) = ku + kv
8. ( k +i) u = ku +lu
9. k(u) = (kl)u
10. 1u = u

contoh soal ruang vektor

Misalkan W = {(x, 0)| x Î R}. Tunjukkan bahwa W adalah subruang dari R2

Bukti:

1. Jelas W Ì R2

Jelas (x, 0) Î W

Jadi W¹Æ

2. Ambil sembarang u = (u1 , 0) dan v = (v1, 0) Î W dan k Î R.

Jelas u + v = (u1 , 0) + (v1, 0) = (u1+v1, 0) Î W

ku = (ku1 , 0) Î W

Jadi W suatu subruang atau ruang bagian dari R2 

 

NILAI EIGEN, VEKTOR EIGEN DAN DIAGONALISASI

Nilai Eigen (${\displaystyle \lambda }$) adalah nilai karakteristik dari suatu matriks berukuran n x n, sementara vektor Eigen (${\displaystyle x}$) adalah vektor kolom bukan nol yang bila dikalikan dengan suatu matriks berukuran n x n akan menghasilkan vektor lain yang memiliki nilai kelipatan dari vektor Eigen itu sendiri.Definisi tersebut berlaku untuk matriks dengan elemen bilangan real dan akan mengalami pergeseran ketika elemen berupa bilangan kompleks. Untuk setiap nilai Eigen ada pasangan vektor Eigen yang berbeda, namun tidak semua persamaan matriks memiliki nilai Eigen dan vektor Eigen.Nilai Eigen dan vektor Eigen berguna dalam proses kalkulasi matriks, di mana keduanya dapat diterapkan dalam bidang Matematika murni dan Matematika terapan seperti transformasi linear.

Kumpulan pasangan nilai dan vektor Eigen dari suatu matriks berukuran n x n disebut sistem Eigen dari matriks tersebut.^[5] Ruang Eigen dari ${\displaystyle \lambda }$merupakan kumpulan vektor Eigen yang berpasangan dengan ${\displaystyle \lambda }$ yang digabungkan dengan vektor nol. Istilah Eigen seringkali diganti dengan istilah karakteristik, di mana kata ‘’’Eigen’’’ yang berasal dari bahasa Jerman memiliki arti ‘’asli’’ dalam konteks menjadi ciri khas atau karakteristik dari suatu sifat.

Syarat-syarat

Nilai dan vektor Eigen sendiri memiliki beberapa syarat yang harus dipenuhi, yaitu:^[3]

• ${\displaystyle (A-\lambda I)}$ tidak memiliki invers atau ${\displaystyle det(A-\lambda I)=0}$
• ${\displaystyle x\neq 0}$

Bukti

${\displaystyle x=Ix}$

Asumsikan bahwa A memiliki invers, maka berlaku ${\displaystyle v}$⁻¹${\displaystyle v=I}$.^[9]

${\displaystyle x=((A-\lambda I)}$^-1 ${\displaystyle (A-\lambda I))x}$

${\displaystyle x=(A-\lambda I)}$^-1 ${\displaystyle ((A-\lambda I)x)}$

${\displaystyle x=(A-\lambda I)}$^-1 ${\displaystyle 0}$

${\displaystyle x=0}$

Rumus

contoh

METODE GOUSS JORDAN

Eliminasi Gauss

adalah suatu metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana lagi. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.

Ciri ciri Metode Gauss adalah 

1. Jika suatu baris tidak semua nol, maka bilangan pertama yang tidak nol adalah 1 (1 utama)
2. Baris nol terletak paling bawah 
3. 1 utama baris berikutnya berada dikanan 1 utama baris diatasnya
4. Dibawah 1 utama harus nol

---

Eliminasi Gauss Jordan

---

Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana lagi. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.

Metode ini digunakan untuk mencari invers dari sebuah matriks.

Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah

1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.

2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks




CONTOH 1



CONTOH 2

MATRIKS OBE

Operasi Baris Elementer (OBE) merupakan suatu operasi yang diterapkan pada baris suatu matriks. OBE bisa digunakan untuk menentukan invers suatu matriks dan menyelesaikan suatu sistem persamaan linear (SPL). 
Operasi Baris Elementer (OBE) adalah salah satu alternatif dalam menyelesaikan suatu bentuk matriks seperti menentukan invers matriks dan penerapan matriks pada sistem persamaan linear menggunakan dua cara yaitu "Eliminasi Gauss" dan "Eliminasi Gauss-Jordan".

Sifat Matriks Hasil OBE

1. Pada baris pertama tidak nol maka unsur tidak nol pertama adalah (dinamakan utama) 
2. Pada baris yang berurutan, baris yang lebih rendah memuat 1 utama yang lebih ke kanan 
3. Jika ada baris nol (baris yang semua unsurnya nol), maka ia diletakan pada baris paling bawah 
4. Pada kolom yang memuat unsur utama, maka entri yang berada diatas dan dibawahnya sedemikian rupa diupayakan menjadi nol  

CATATAN :

• Matriks hasil OBE dinamakan eselon baris jika dipenuhi sifat 1,2 dan 3 (Proses Eliminasi Gauss) 
• Matriks hasil OBE dinamakan eselon baris tereduksi jika dipenuhi semua sifat (Proses Eliminasi Gauss-Jordan)

CONTOH SOAL

MATRIKS ELEMENTER

Matriks elementer adalah matrik yang diperoleh dari operasi elementer yang dikenakan pada matrik identitas. Setiap matrik elementer mempunyai invers, dan setiap matrik bujur sangkar berordo (nxn) yang mempunyai invers ekivalen baris terhadap matrik identitas I. 

contoh soal :

PARTISI MATRIKS

PARTISI MATRIKS

• Matriks partisi adalah membagi matriks menjadi beberapa matriks yang ukurannya lebih kecil dengan memasukan garis horizontal dan vertikal antara baris dan kolom matriks.

• Matriks-matriks yang ukurannya kecil hasil partisi matriks disebut sub matriks.

• Partisi matriks digunakan untuk menyederhanakan matriks yang ukurannya besar menjadi matriks kecil sehingga lebih mudah dioperasikan untuk tujuan tertentu.

• Setiap sub matriks hasil partisi selalu dapat dikembalikan ke dalam matriks asalnya.

CONTOH 

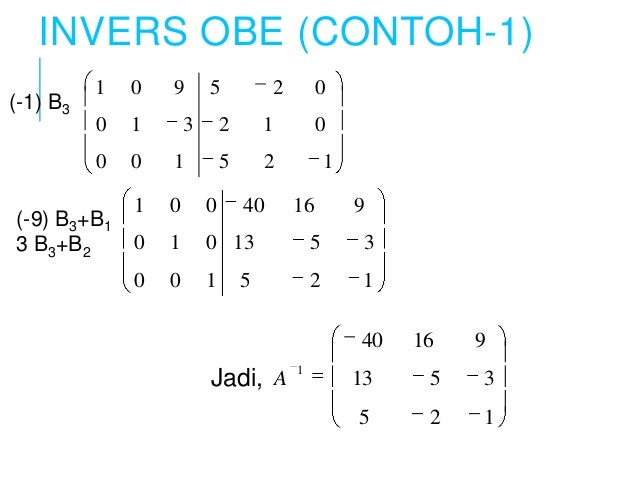
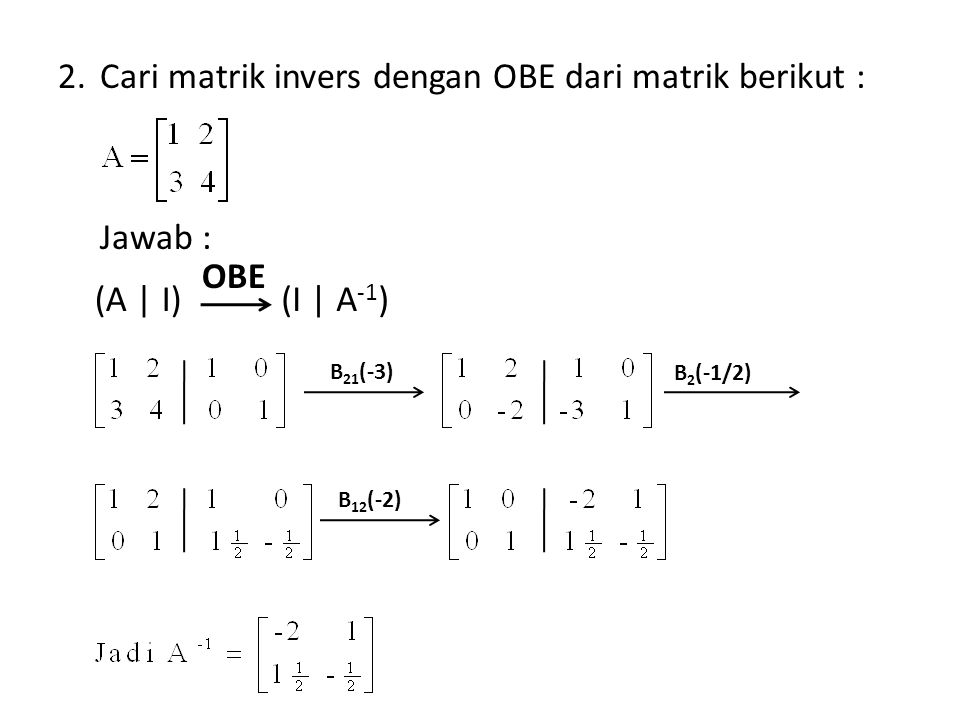
CONTOH SOAL