- Determinan Matriks
determinan adalah sebuah nilai yang dapat dihitung dari unsur suatu matrikspersegi
Determinan Matriks A ditulis dengan sebuah tanda, det(A), , atau ||
- Determinan Matriks Ordo 2 x 2
matriks ordo 2 dinyatakan seperti bentuk di bawah.
Nilai determinan A disimbolkan dengan  , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
Contoh Soal:
, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
Contoh Soal:
Tentukan nilai determinan matriks
Pembahasan:
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
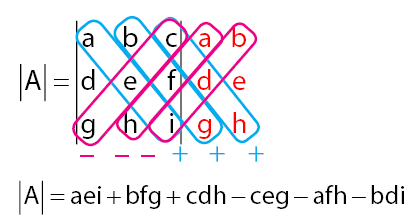 Contoh perhitungan determinan pada matriks ordo 3:
Maka,
Contoh perhitungan determinan pada matriks ordo 3:
Maka,
Tentukan nilai determinan matriks
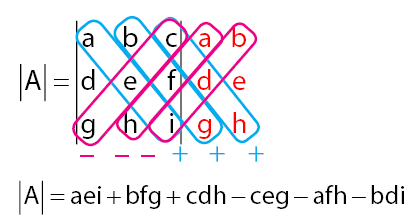
- Kofaktor
Kofaktor merupakan salah satu langkah yang biasanya kita lakukan dalam mencari invers suatu matriks. Dan ini memiliki kelebihan dibandingkan dengan mencari determinan matriks dengan metode sarrus.jika pada metode sarrus, kita hanya bisa mencari determinan suatu matriks sampai pada ordo 3 x 3.


- Minor
Minor matriks adalah determinan matriks bagian dari matriks yang diperoleh dengan cara menghilangkan elemen pada baris tertentu dan elemen pada kolom tertentu.
cara mencari determinan dari elemen-elemen matrix yang tidak terkena oleh garis orange. Dan untuk letak tiap minornya adalah bergantung pada elemen yang menjadi titik pertemuan antara orange.

Minor matriks adalah determinan matriks bagian dari matriks yang diperoleh dengan cara menghilangkan elemen pada baris tertentu dan elemen pada kolom tertentu.
cara mencari determinan dari elemen-elemen matrix yang tidak terkena oleh garis orange. Dan untuk letak tiap minornya adalah bergantung pada elemen yang menjadi titik pertemuan antara orange.
- Sifat-Sifat Determinan Matriks
- Jika matriks A sembarang yang semua elemen dalam salah satu baris atau kolomnya adalah nol, maka determinan A = 0.
Contoh matriks 2×2
| Baris | Kolom |
Contoh matriks 3×3
| Baris | Kolom |
- Jika matriks A sembarang adalah matriks segitiga atas, matriks segitiga bawah, atau matriks diagonal, maka determinan A = hasil kali elemen diagonal utama.
Contoh matriks 2×2
| Segitiga Atas | Segitiga Bawah |
| Diagonal |
Contoh matriks 3×3
| Segitiga Atas | Segitiga Bawah |
| Diagonal |
- Jika matriks A’ adalah matriks yang diperoleh dari matriks A setelah salah satu baris/kolomnya dikalikan dengan konstanta k, maka determinan A’ = k x Det A.
| Matriks A |
| A' (Baris) | A'(kolom) |
Contoh matriks 3×3
| Matriks B |
| B'(Baris) |
| B'(kolom) |
- Jika matriks A’ dihasilkan dari matriks A setelah dua baris/kolomnya ditukarkan, maka determinan A’ = – det A.
Contoh matriks 2×2
| Matriks A |
| Tujar Baris | Tukar Kolom |
Contoh matriks 3×3
| Matriks B |
| Tukar Baris |
| Tukar kolom |
- Jika A’ adalah matriks yang dihasilkan dari matriks A setelah salah satu baris/kolomnya dikalikan dengan konstanta kemudian dijumlahkan/dikurangkan terhadap baris/kolom yang lainnya, maka determinan A’ = determinan A.
| Matriks A |
| Baris | Kolom |
Contoh matriks 3×3
| Matriks B |
| Baris |
| Kolom |
- Jika sebuah matriks mempunyai dua baris yang elemen-elemennya sebanding, maka determinannya adalah nol.
| Dua Baris Sama |
| Baris Sebanding | Kolom Sebanding |
Contoh matriks 3×3
| Dua Baris Sama |
| Baris Sebanding |
| Kolom Sebanding |
- Suatu matriks nilai determinannya tidak akan berubah jika barisnya dijadikan kolom.Dengan kata lain determinan matriks asal sama dengan determinan matriks hasil transpose.
Contoh matriks 2×2
| Matriks A | Transpose A |
Contoh matriks 3×3
| Matriks B |
| Baris Sebanding |